그래프

2개 이상의 항목이 어떤 관계를 맺고 있는지를 노드(정점)와 에지(선)을 이용해서 표현하는 것을 그래프라고 한다. 페이스북이나 트위터에서 각 사용자가 다른 사용자와 어떤 관계를 맺는지 표현하는 경우가 그래프를 사용하는 대표적인 예이다.

1. 깊이 우선 탐색과 너비 우선 탐색

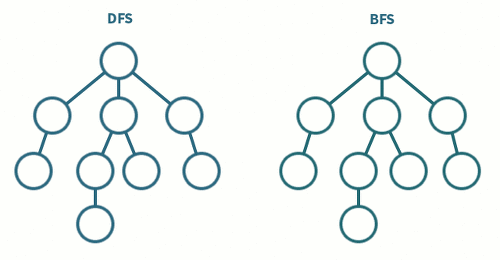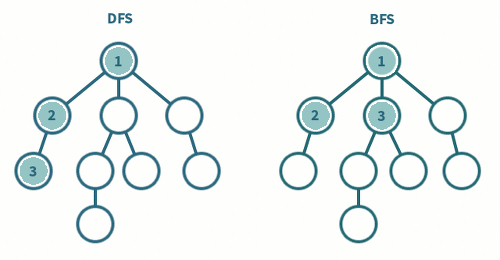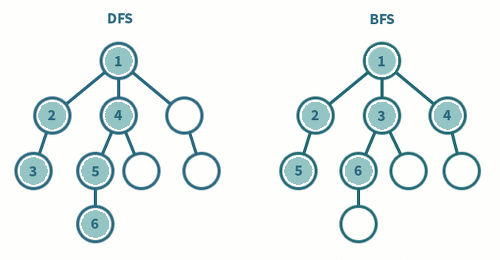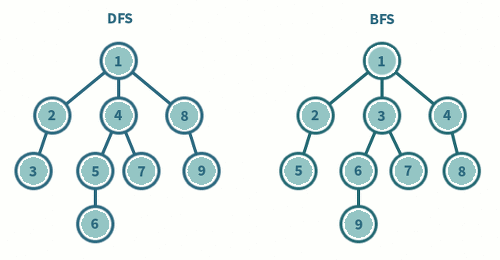
1.1 깊이 우선 탐색 (DFS; Depth First Search)

시작 정점에서 한 방향으로 갈 수 있는 가장 먼 경로까지 탐색하다가 갈 곳이 없으면, 가장 마지막에 만났던 부모 노드로 돌아와서 다른 방향을 탐색하는 방법

1.2 너비 우선 탐색 (BFS; Breadth First Search)

시작 정점에서 인접한 모든 정점들을 우선 방문한 후, 더 이상 방문하지 않은 정점이 없을 때까지 방문했던 정점들을 다시 시작점으로 해서 모든 정점들을 차례로 방문하는 방법

2. 신장 트리와 최소 신장 트리

2.1 신장 트리

그래프 안의 모든 정점을 포함하는 트리이며, 모든 정점들이 연결되어 있어야 하고 사이클을 포함하지 않는다.

2.2 최소 비용 신장 트리

가중치가 부여된 무방향 그래프에서 신장 트리 비용의 최소화를 구하는 방법을 말한다. 주로 사용되는 방법은 다음과 같다.

• Prim 방법
  • 시작하는 노드에 연결된 것 중에서 가중치가 최소인 노드를 선정한다.
  • 선정된 노드에 연결된 것 중에서 가중치가 최소인 것을 선정한다.
  • 이어진 노드에서 최솟값을 계속 선정한다.
• Kruskal 방법
  • 전체 그래프를 보고 최소 가중치를 선정한다.
  • 그 다음 최소 가중치를 가지는 것을 선정한다.
  • 선정할 때 사이클을 구성하는 것이 있으면 제외하고 작업을 진행한다. 동일한 것이 여러 개 있으면 임의로 하나를 선정해서 진행한다.

3. 그래프를 사용하는 대표적인 두 가지 방법

• PERT/CPM
  • Program Evaluation and Review Technique/Critical Path Method의 약자로, 비용을 적게 사용하면서 최단 시간 안에 계획을 완성하기 위한 프로젝트 일정 관리 기법이다.
• 최단 경로
  • 그래프에서 정점 a,b를 연결하는 경로 중에 가중치의 합이 최소가 되는 경로를 찾는 방법이다.
  • 데이크스트라(Dijkstra) 알고리즘이 대표적이다.

Table of contents

• 너비 우선 탐색(BFS)
• 깊이 우선 탐색(DFS)
• 다익스트라 알고리즘