너비 우선 탐색(BFS)
BFS(Breadth-First Search)는 그래프 전체를 탐색하는 방법 중의 하나로, 루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법이다. 여기서 그래프란 연결의 집합을 모형화한 것이다. 그래프는 정점과 간선으로 이루어져있다.
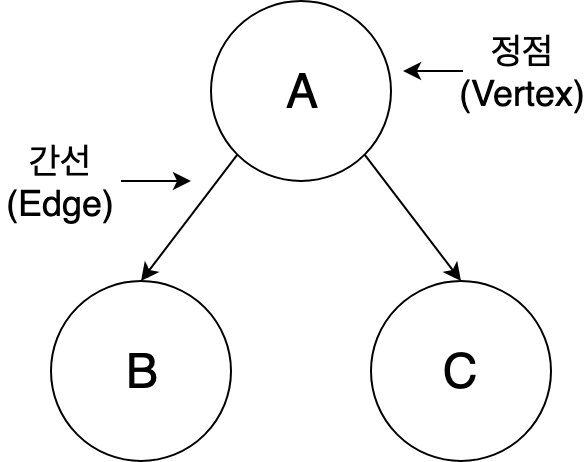
정점은 여러 개의 다른 정점과 바로 이어질 수 있다. 이렇게 바로 이어진 정점을 이웃이라고 한다. 이 그래프에서 A와 B, A와 C는 서로 이웃이다. B와 C는 이어져 있지 않기 때문에 알렉스의 이웃이 아니다.
너비 우선 탐색을 사용하면 두 항목 간의 최단 경로를 찾을 수 있다. 그런데 이 최단 경로라는 말은 여러 가지를 의미할 수 있다.
- 체커 게임에서 가장 적은 수로 승리할 수 있는 방법을 계산하는 인공지능
- 맞춤법 검사기 (실제 단어에서 가장 적은 개수의 글자를 고쳐서 올바른 단어를 만드는 방법을 찾는다)
- 주변에서 가장 가까운 샤브샤브집 찾기
정점과 간선
BFS의 목적은 임의의 정점에서 시작해서 모든 정점을 한 번씩 방문하는 것이다. 너비 우선 탐색은 아래와 같은 질문에 대해 대답할 수 있어야 한다.
- 정점 A에서 정점 B로 가는 경로가 존재하는가?
- 정점 A에서 정점 B로 가는 최단 경로는 무엇인가?
그렇다면 각 정점과 간선은 어떻게 표현할까? 바로 해시 테이블을 사용하면 된다. 위의 그림을 해시 테이블로 표현하면 다음과 같다.
graph = {}
graph["A"] = ["B", "C"]
graph["B"] = []
graph["C"] = []
print(graph)
# {'A': ['B', 'C']}
만약 B와 C가 자식을 가지고 있다면, A와 마찬가지로 배열에 자식을 가지고 있을 것이다.
Queue로 BFS를 구현하는 방법
BFS를 구현하기 위해서는 선입선출(FIFO)을 원칙으로 하는 큐(Queue)를 사용한다. 일반적으로 큐를 이용해서 반복적인 형태로 구현하는 것이 가장 잘 동작한다.
- Queue의 가장 앞에 있는 노드를 Pop
- 현재 노드에 인접한 모든 노드들 중 아직 방문하지 않은 노드들을 Queue에 Push
- Queue가 비어있지 않으면 1번부터 다시 실행
여기서 push는 나중에 방문할 노드를 저장하는 것이고, pop은 front에 있는 노드를 방문하는 것이다. 이 논리구조를 간략하게 나타내면,
while(Queue가 비어있지 않은 동안) {
1. Queue의 가장 앞에 있는 노드를 pop
2. 현재 노드에 인접한 모든 노드들 중 아직 방문하지 않은 노드들을 Queue에 Push
}
문제
로봇 청소기
- 최소 거리를 구하는 거니까 BFS로 구할 수 있음
- 칸을 이동할 때는 한 번으로 셈
- 모든 최단거리는 시작점이 1개일 때 다른 모든 거리의 최단거리를 구하는 알고리즘임. 그 말은 시작점이 고정이 되면 최단거리를 여러 번 구할 필요가 없음. 하지만 이 문제는 시작점이 한 개가 아님.
- 더러운 칸의 개수는 10개를 넘지 않는다 조건 때문에 BFS로 구할 수 있음. 경우의 수는 10!
레이저 통신
- 가중치를 의미하는 건 선분의 갯수
- 가중치는 0 아니면 1
0과 1
- 경우의 수가 많아서 브루트 포스로는 안 됨
점프 게임
- 이동방법은 총 3개
- 앞으로 뒤로 다른 칸으로 점프
- 거리가 -1이면 이미 방문한 곳임
- 이동할 수 없으면 0 이동할 수 있으면 1
- 내가 이동하려는 칸보다 최소시간이 크면 못 가는 칸이라고 처리