다익스트라 알고리즘
너비 우선 탐색(이하 BFS)가 최단 경로를 구하는 알고리즘이라면, 다익스트라 알고리즘은 가장 빠른 경로를 구하는 알고리즘이다.
다익스트라 알고리즘을 사용할 때, 그래프의 각 간선은 어떤 숫자를 가진다. 이 숫자를 가중치(weight)라고 한다. 참고로 가중치를 가지는 그래프를 가중 그래프(weighted graph)라고 한다. 가중치가 없는 그래프는 균일 그래프(unweighted graph)라고 한다. 균일 그래프에서 최단 경로를 계산할 때는 BFS를 사용한다. 그래프는 사이클이라는 가지고 있을 수도 있는데, 사이클이란 그래프가 어떤 정점에서 출발해 한 바퀴 돌아 같은 정점에서 끝나는 것이다.
다익스트라 알고리즘의 포인트는 그래프에서 가장 가격이 싼 정점을 찾는 것이다. 그 가격보다 더 싸게 그 정점에 도달하는 방법은 없다.
음의 가중치가 있으면 다익스트라 일고리즘을 사용할 수 없다. 만약 음의 가중치를 가진 그래프에서 최단 경로를 찾고 싶다면 벨만-포드 알고리즘을 사용하면 된다.
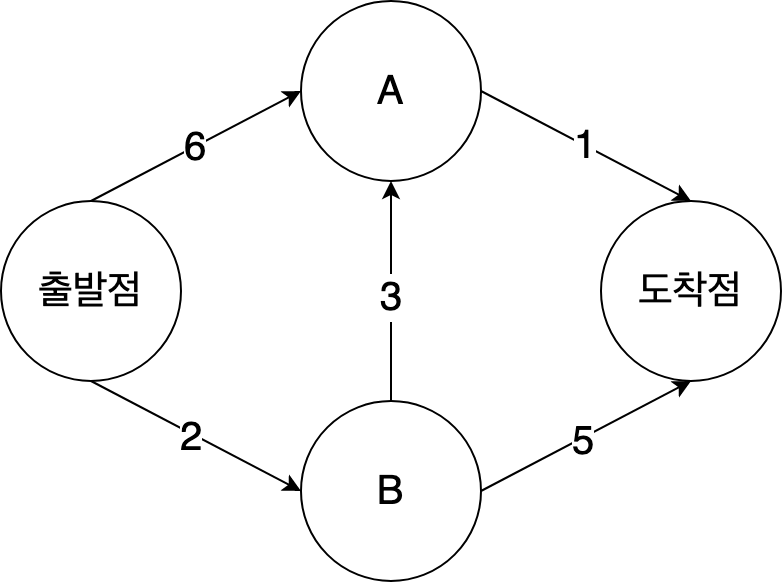
각 구간은 분 단위로 표시한 이동 시간을 가진다. 다익스트라 알고리즘을 사용해서 출발점에서 도착점으로 가는 가장 최단 시간 경로를 구해보자.
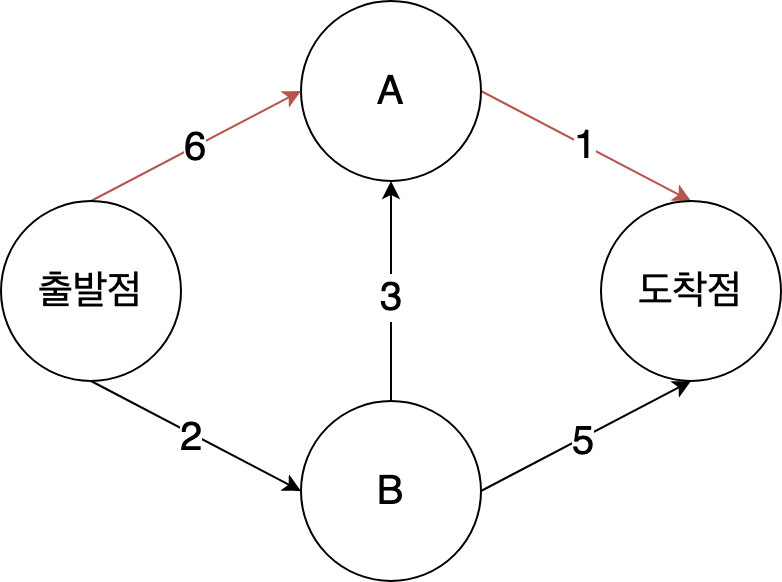
만약 너비 우선 탐색을 사용한다면 7분이 걸린다. 7분은 가장 빠른 시간이 아닌데 어떻게 최단 경로를 찾을 수 있을까?
다익스트라 알고리즘의 단계
다익스트라 알고리즘은 4단계로 이루어진다.
- 가장 가격이 싼 정점을 찾는다. 가장 가격이 싼 정점이란 도달하는 데 시간이 가장적게 걸리는 정점을 말한다.
- 이 정점의 이웃 정점들의 가격을 조사한다.
- 그래프 상의 모든 정점에 대해 이러한 일을 반복한다.
- 최종 경로를 계산한다.
이 단계를 위 그래프에 적용해보자.
1단계
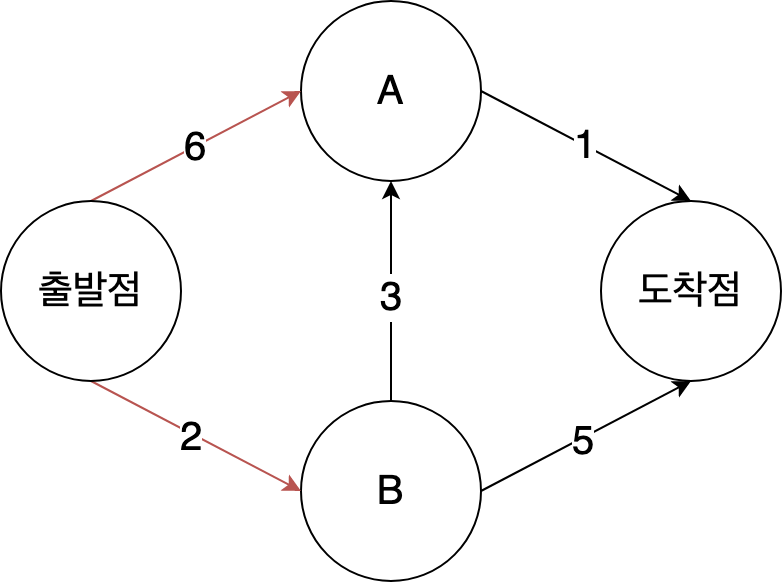
가장 싼 정점을찾는다. 정점 A로 가는 데에는 6분이 걸리고, 정점 B로 가는데에는 2분이 걸린다. 나머지 정점에 대해서는 아직 알지 못한다. 도착점까지 가는 데 얼마나 걸리는지는 아직 알 수 없기 때문에 일단 무한대라고 가정하자. 지금까지는 정점 B가 가장 가까우며 2분이 걸린다.
| 정점 | 소요시간 |
|---|---|
| A | 6 |
| B | 2 |
| 도착점 | 무한대 |
2단계
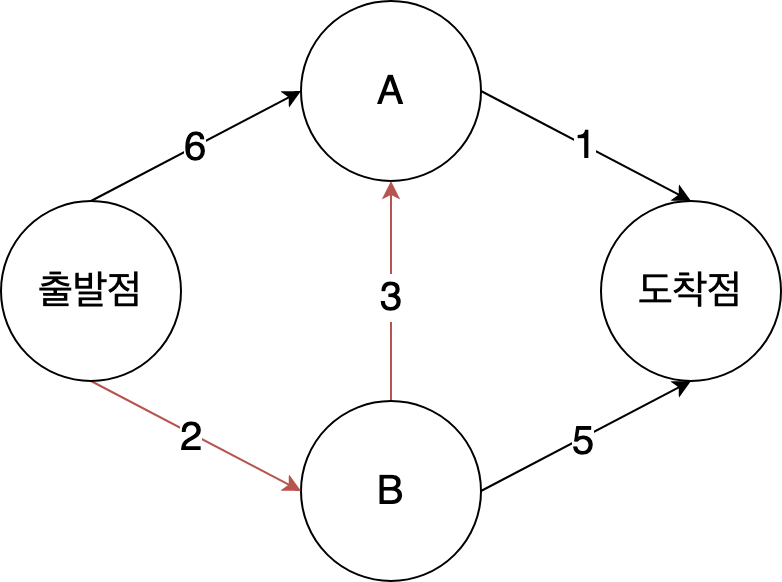
정점 B의 모든 정점에 대해 B를 통과하여 점점 A에 도달하는 데 걸리는 시간을 계산한다.
| 정점 | 소요시간 |
|---|---|
| A | 5 |
| B | 2 |
| 도착점 | 7 |
A의 값이 6에서 5로 바뀌었다. 정점 A에 다다르는 빠른 경로를 찾았기 때문이다. 정점 B의 이웃 정점에 대해 더 빠른 경로를 찾으면 가격을 바꾼다. 이 경우에는 다음과 같은 경로를 찾았다.
- 정점 A로 가는 더 짧은 거리 (6분에서 5분으로 수정)
- 도착점까지 가는 더 짧은 거리 (무한대에서 7분으로 수정)
3단계
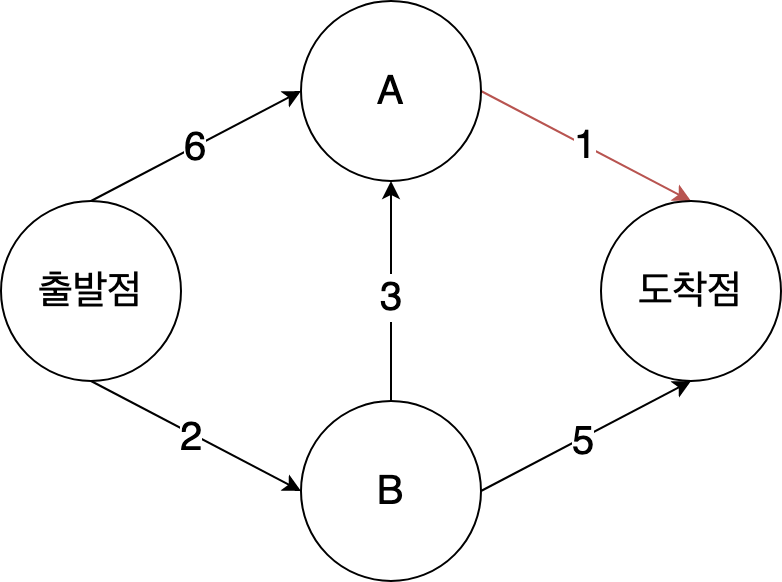
지금까지 한 일을 반복한다. 정점 B는 이미 처리했고, 정점 A가 그 다음으로 시간이 적게 걸린다. 정점 A를 조사해 A의 이웃 정점에 대한 가격을 수정한다.
| 정점 | 소요시간 |
|---|---|
| A | 5 |
| B | 2 |
| 도착점 | 6 |
이제 모든 정점에 대해 다익스트라 알고리즘을 돌려보면 다음과 같이 나온다.
- 정점 B에 도달하는 데는 2분이 걸린다.
- 정점 A에 도달하는데는 5분이 걸린다.
- 도착점에 도달하는 데는 6분이 걸린다.
4단계
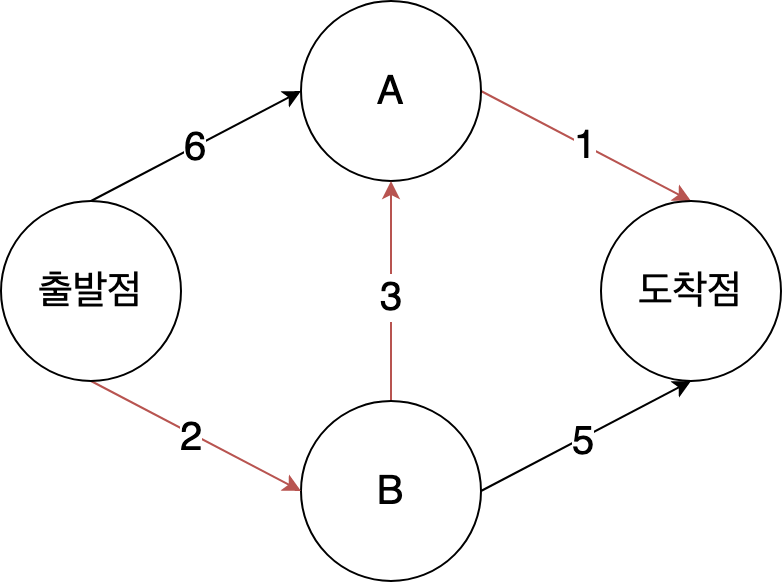
최종 경로를 계산한다.
구현
위 단계를 구현하려면 3개의 해시 테이블이 필요하다
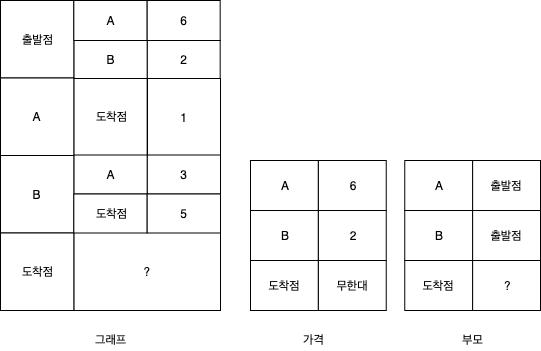
- 그래프에 대한 해시 테이블
- 가격에 대한 해시 테이블
- 부모에 대한 해시 테이블
알고리즘을 실행하면서 해시 테이블과 부모 해시 테이블을 갱신하게 된다.

- 모든 정점을 처리할 때까지 반복한다.
- 출발점에서 가장 가까운 정점을 찾는다.
- 이웃 정점의 가격을 갱신한다.
- 만약 이웃 정점의 가격을 갱신하면 부모도 갱신한다.
- 해당 정점을 처리했다는 사실을 기록한다.
- 1로 돌아간다.
# the graph
graph = {}
graph["start"] = {}
graph["start"]["a"] = 6
graph["start"]["b"] = 2
graph["a"] = {}
graph["a"]["fin"] = 1
graph["b"] = {}
graph["b"]["a"] = 3
graph["b"]["fin"] = 5
graph["fin"] = {}
# the costs table
infinity = float("inf")
costs = {}
costs["a"] = 6
costs["b"] = 2
costs["fin"] = infinity
# the parents table
parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["fin"] = None
processed = []
def find_lowest_cost_node(costs):
lowest_cost = float("inf")
lowest_cost_node = None
# 모든 정점을 확인한다.
for node in costs:
cost = costs[node]
# 아직 처리하지 않은 정점 중 더 싼 것이 있다면
if cost < lowest_cost and node not in processed:
# 새로운 최저 정점으로 설정한다.
lowest_cost = cost
lowest_cost_node = node
return lowest_cost_node
# 아직 처리하지 않은 가장 싼 정점을 찾는다.
node = find_lowest_cost_node(costs)
# 모든 정점을 처리하면 반복문이 종료된다.
while node is not None:
cost = costs[node]
# 모든 아웃에 대해 반복한다.
neighbors = graph[node]
for n in neighbors.keys():
new_cost = cost + neighbors[n]
# 만약 이 정점을 지나는 가격이 더 싸다면
if costs[n] > new_cost:
# 정점의 가격을 갱신하고
costs[n] = new_cost
# 부모를 이 정점으로 새로 갱신한다.
parents[n] = node
# 정점을 처리한 사실을 기록한다.
processed.append(node)
# 다음으로 처리할 정점을 찾아 반복한다.
node = find_lowest_cost_node(costs)
print("Cost from the start to each node:")
print(costs)
References
- 그림으로 개념을 이해하는 알고리즘